Tôi là một người may mắn vì từng là học trò và là đồng nghiệp của thầy Lê Bá Khánh Trình tại trường PTNK. Sau các năm học và giảng dạy tại trường, tôi học hỏi được ở thầy nhiều điều, đối với tôi thầy là thầy giáo giỏi và sống rất giản dị. Ở trường PTNK hiện nay, thầy là tổ trưởng tổ toán đồng thời phụ trách môn hình học của các lớp chuyên và đội tuyển. Thầy chưa xuất bản quyển sách nào cho riêng mình về hình học, chỉ có những bài giảng được trình bày trong các hội thảo hay trại hè. Tôi có được bản viết tay một bài báo hay của thầy, bài viết được trình bày trong hội thảo toán học sơ cấp và đăng trong kỷ yếu trại hè năm 2009. Tôi xin được đăng lại để các bạn yêu thích hình học tham khảo.
-
Hình học tĩnh hay động
Trong bài này, tôi muốn trình bày một đôi điều riêng tư về môn hình học phổ thông (hay còn được gọi là hình học sơ cấp) dưới hai cách nhìn có phần nào khác biệt nhau. Trước hết, thông dụng hơn cả là cách nhìn của một người quan tâm đến việc giải các bài toán hình học. Cách nhìn này thường yêu cầu xem xét, phân loại các bài toán khác nhau, trình bày kinh nghiệm giải quyết chúng và tìm ra các mối liên quan giữa chúng với các bài toán đã biết. Cách nhìn này thường được quan tâm hàng đầu và thường là nội dung chính trong các bài viết, các tài liệu về toán phổ thông. Bên cạnh đó, tôi cũng muốn trình bày các vấn đề ở đây dưới một cách nhìn khác, cách nhìn của người muốn tìm tòi, phát hiện ra các bài toán mới, những bài toán không chỉ mới về nội dung mà còn có tác dụng tích cực trong việc rèn luyện tư duy và các kỹ năng cần thiết của người học, đặc biệt là đối với những học sinh giỏi. Đây là công việc đòi hỏi ở chúng ta nhiều công phu không kém gì công việc giải quyết các bài toán. Tuy nhiên, ở nước ta dường như công việc này còn chưa được quan tâm đúng mức. Đây đó, được ưa chuộng hơn cả vẫn là sử dụng các bài toán hay, mẫu mực đã có hoặc tận dụng các đề toán mới được công bố ở các nước khác. Cách làm này khá tiện lợi, hợp lý và hiệu quả nhưng thực tế có hai nguy cơ:
-
Một là, nếu sử dụng các bài toán đã được công bố trong các kỳ thi, việc đánh giá sẽ thiếu công bằng và chính xác;
-
Hai là, đáp án của nhiều bài toán do vô tình hay hữu ý, đã ít nhiều bị biến dạng. Điều này có thể làm cho cách trình bày trở nên ngắn gọn hơn nhưng đồng thời cũng đã làm mất đi những ý tưởng trong sáng và tự nhiên ban đầu khi những bài toán đó được xây dựng nên. Vì thế, nếu sử dụng lại các đáp án một cách máy móc, thiếu sự biên tập cần thiết thì rất có thể chúng sẽ có tác dụng tiêu cực đến việc rèn luyện tư duy của người học.
Với những suy nghĩ đó, tôi nghĩ chắc cũng đã đến lúc chúng ta cần tăng cường sự quan tâm và đầu tư nhiều công sức hơn nữa cho công việc “sáng tác” này. Một công việc không dễ dàng nhưng chắc chắn sẽ rất thú vị và bổ ích. Bây giờ, đã đến lúc đi thẳng vào chủ đề của bài này: Hình học tĩnh hay động? Nếu chỉ nhìn các bài toán mà chúng ta vẫn thường giải quyết hoặc tìm tòi thì hình học vừa tĩnh lại vừa động. Hình học tĩnh trong những bài toán mà ở đó, các yếu tố như điểm, đường thẳng, đường tròn,… đều không thay đổi và yêu cầu đặt ra ở đây thường là chứng minh các tính chất hình học hoặc tính toán các đại lượng nào đó trong hình vẽ đã cho. Còn hình học sẽ động trong những bài toán mà ở đó, bên cạnh các yếu tố cố định, không thay đổi có 1 vài yếu tố thay đổi và yêu cầu ở đây thường là tìm quĩ tích, tìm các điểm cố định hoặc tìm giá trị lớn nhất, nhỏ nhất của một đại lượng hình học. Tuy nhiên, đây chỉ là cái nhìn ban đầu. Trên quan điểm của những người mong muốn đi tìm lời giải cho các bài toán khó và cả trên quan điểm của những người mong muốn phát hiện ra những bài toán hình học mới, theo tôi, hình học luôn luôn cần vận động, vận động ngay cả trong những bài toán mà các yếu tố được cho đều cố định, không đổi. Bởi vì chính cách nhìn, cách tư duy trong các yếu tố của hình vẽ không ngừng biến động, tuơng tác, thậm chí toàn bộ cả hình vẽ đều không thay đổi sẽ giúp chúng ta tìm ra đúng những lời giải đẹp nhất và phản ánh trọn vẹn nhất bản chất hình học của một bài toán.
2. Động trong biến hình
Một trong những công cụ quan trọng hàng đầu để thực hiện việc biến đổi các yếu tố trong một hình chính là phép biến hình. Không phải ngẫu nhiên mà hiện nay, những lời giải hay nhất của nhiều bài toán hình học cũng như rất nhiều phát hiện hình học thú vị thường nhận được trên cơ sở vận động ý tưởng và kỹ thuật của các phép biến hình.
Thế nhưng để có thể vận dụng chúng một cách hiệu quả, trước hết phải có được một nền tảng tương đối vững chắc về biến hình mà cụ thể là phải nắm bắt được một vài mệnh đề quan trọng và làm quen được với một số tình huống tiêu biểu cho việc thực hiện các động tác biến hình hợp lý.
Vậy đó là những mệnh đề nào, những tình huống nào? Trong khuôn khổ bài này, tôi chỉ xin phép trình bày những gì liên quan đến phép quay, một loại phép biến hình tuy đơn giản nhưng lại có mức độ áp dụng cao và mang lại rất nhiều kết quả phong phú. Tương tự, không khác biệt với phép quay bao nhiêu là phép vị tự quay. Thông thường, phép vị tự quay đem lại các kết quả tổng quát hơn và nâng cao độ phức tạp của bài toán mà vẫn giữ nguyên ý tưởng ban đầu của phép quay.
Nhưng trước khi phát biểu ra đây các mệnh đề, tình huống cần thiết được nhắc ở trên, xin phép được nói qua một chút cái gọi là “cảm hứng” thúc đẩy tôi viết ra những dòng này. “Cảm hứng” đó nảy sinh từ việc xem xét giáo trình Hình học nâng cao lớp 11 vừa được đưa vào giảng dạy từ vài năm học vừa qua, trong đó điểm đáng lưu ý nhất là phần các phép biến hình được trình bày đầy đủ hơn và đặc biệt là đã được phân bố ngay vào đầu năm học (trước đây, phần này chỉ được giảng dạy vào cuối năm lớp 10). Rõ ràng, với sự thay đổi này, hội đồng biên soạn sách giáo khoa cho thấy ý định rất nghiêm túc của mình là tăng cường hơn nữa sự chú ý cho phần các phép biến hình và đây thực sự là điều rất nên làm.
Các phép biến hình chính là mảng kiến thức mà ở đó, học sinh có thể làm được với những ý tưởng và những kỹ năng thích hợp nhất cho việc tiếp thu các kiến thức của toán học hiện đại. Những ý tưởng và những kỹ năng đó là gì? Đó là ý tưởng ánh xạ rất rõ nét trong cách trình bày và hệ thống các phép biến hình. Đó là ý tưởng phân loại và mô tả đầy đủ các lớp phép biến hình (mà tiêu biểu nhất là các phép dời hình). Và tất nhiên, quan trọng hơn cả là qua việc vận dụng các phép biến hình để giải toán, tư duy hình học của học sinh sẽ được nâng lên ở một cấp độ mới. Thay vì chỉ biết tính toán và so sánh các đại lượng hình học (góc, độ dài, diện tích,… ) để từ đó đi đến một chứng minh như trước đây, nay với việc sử dụng các phép biến hình, các em sẽ được tập quan sát những vận động, những tương tác giữa các yếu tố, những cấu trúc tiềm ẩn trong một hình vẽ để rồi từ đó rút ra được những chứng minh, những kết luận sâu sắc, nêu bật toàn diện bản chất của hình vẽ đó.
Những ý định như vậy là rất đúng đắn và chắc cũng đã được hội đồng biên soạn sách giáo khoa đem ra cân nhắc kỹ lưỡng trước khi quyết định việc phân bố lại chương trình sách giáo khoa nâng cao về hình học. Chỉ tiếc một điều, theo nhận xét chủ quan của tôi, là nội dung trình bày trong sách giáo khoa lớp 11 có lẽ vẫn còn chưa đủ để học sinh rèn luyện, nắm bắt và vận dụng công cụ biến hình ở mức độ cần thiết, ít ra là chưa cho phép các em làm quen được với ba ý tưởng quan trọng và bổ ích được kể ra ở trên.
Vậy nên cần bổ sung những điều gì? Xin điểm qua một vài điều tôi cho là quan trọng nhất và nhân tiện, đây cũng chính là trả lời cho câu hỏi đặt ra ở đầu phần này. Đó là phát biểu các mệnh đề, các tình huống chính mà bất cứ ai khi học các phép toán biến hình (cụ thể là phép quay) đều phải biết để có thể vận dụng thực sự tốt công cụ này.
2.1. Sự tồn tại của phép quay. Trước hết, để giúp cho học sinh hiểu rõ và tự tin hơn khi sử dụng các phép biến hình, nên trang bị cho các em các mệnh đề về tồn tại duy nhất của một phép biến hình trong những tình huống đơn giản và thông dụng nhất. Đối với phép quay, mệnh đề sau đáp ứng đủ các yêu cầu đó.
 Mệnh đề 2.1. Cho hai đoạn thẳng AB và A’B’ sao cho AB = A’B’ và $latex \overrightarrow{AB} \neq \overrightarrow{A’B’}$. Khi đó, tồn tại duy nhất một phép quay R biết AB thành A’B’ tương ứng.
Mệnh đề 2.1. Cho hai đoạn thẳng AB và A’B’ sao cho AB = A’B’ và $latex \overrightarrow{AB} \neq \overrightarrow{A’B’}$. Khi đó, tồn tại duy nhất một phép quay R biết AB thành A’B’ tương ứng.
Mệnh đề này cho phép ta chỉ cần quan sát thấy có hai đoạn thẳng bằng nhau là có thể liên tưởng ngay đến một phép quay và sẵn sàng vận dụng nó nếu có thêm các điều kiện thích hợp chứ không phải chờ đến khi có được hai tam giác, hai hình bằng nhau mới bắt đầu nghĩ đến phép quay. Ngoài ra, mệnh đề này còn là cơ sở để mô tả đầy đủ các phép dời hình (sẽ đề cập ở dưới). Tuy nhiên, nó chỉ có ý nghĩa giúp ta làm quen với tình huống. Muốn mang lại hiệu quả thực sự phải bổ sung thêm một ít về việc xác định phép quay tồn tại nói trên.
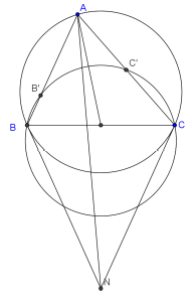
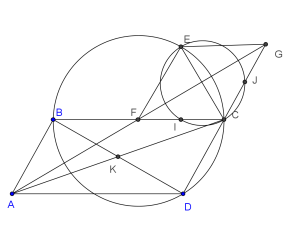
Mệnh đề 2.2. (Mệnh đề 1 bổ sung) Phép quay R có góc quay là $latex \alpha = \widehat{(\overrightarrow{AB}, \overrightarrow{A’B’})} $ và tâm $latex O$ đồng thời nằm trên các trung trực của AA’ và BB’ cũng như các cung tròn (đơn) chứa các điểm nhìn đoạn $latex AA’, BB’$ dưới một góc có hướng bằng $latex \alpha$
Bổ sung này cho ta một cái nhìn khá toàn diện về tình huống đang xét (xem hình vẽ); nhưng để có được sự quan sát đầy đặn và sâu sắc hơn nữa, cần trang bị thêm:
Mệnh đề 2.3. Ta giữ các giả thiết như mệnh đề 2.1 và mệnh đề 2.2. (1) giả sử các đường thẳng AB và A’B’ cắt nhau tại P, khi đó các tứ giác $latex APOA’, BPOB’$ nội tiếp. (2) Giả sử các đường thẳng $latex AA’, BB’$ cắt nhau tại Q, khi đó các tứ giác $latex ABOQ, A’B’OQ$ nội tiếp.
Các mệnh đề này rõ ràng là chứng minh không khó (nên xin bỏ qua ở đây). Còn lợi ích mà chúng có thể mang lại thì lại khá phong phú. Xin bắt đầu bằng một bài tập khá quen thuộc trong đó việc vận dụng ý tưởng biến hình là rất tự nhiên và đơn giản.
Ví dụ 2.4. Cho tam giác ABC cân tại A . Trên cạnh AB và AC lần lượt lấy các điểm M,N sao cho AM = CN. Chứng minh đường tròn ngoại tiếp tam giác AMN luôn đi qua một điểm cố định khác A.
 Lời giải. Xét phép quay biết đoạn thẳng AM tương ứng thành đoạn thẳng CN. Tâm quay O theo mệnh đề 2.2 là giao điểm của đường trung trực và cung tròn quỹ tích những điểm K sao cho:
Lời giải. Xét phép quay biết đoạn thẳng AM tương ứng thành đoạn thẳng CN. Tâm quay O theo mệnh đề 2.2 là giao điểm của đường trung trực và cung tròn quỹ tích những điểm K sao cho:
$latex \widehat{(\overrightarrow{KA}, \overrightarrow{KC})} = \widehat{(\overrightarrow{AM}, \overrightarrow{CN} )}$,
nên tâm quay O cố định. Cuối cùng do AM và CN cắt nhau tại A, nên tứ giác AMON nội tiếp. Vậy đường tròn ngoại tiếp tam giác AMN đi qua điểm O cố định.
Bài tập này rất thích hợp cho việc làm quen với các ứng dụng của phép quay. Nó chỉ có một khiếm khuyết là nếu tam giác ABC cân thì điểm O cần tìm chính là tâm đường tròn ngoại tiếp tam giác ABC . Do đó, nhiều học sinh có thể mày mò, dự đoán và chứng minh kết quả trên mà không cần sử dụng phép quay. Thực ra, để khắc phục điều này, có thể xem tam giác ABC không cân và còn tổng quát hơn là bài tập sau mà cách giải không có gì thay đổi.
Ví dụ 2.5. Trên hai tia $latex Ox$ và $latex Oy$ của góc $latex xOy$, hai điểm A, B. M, N là hai điểm thay đổi trên $latex Ox, Oy $ sao cho $latex AM = BN$ (M khác phía O đối với A, còn N cùng phía O đối với B). Chứng minh rằng đường tròn ngoại tiếp tam giác OMN luôn đi qua điểm cố định khác O.

Nếu bổ sung vào bài tập này thêm một vài yếu tố với những mối quan hệ tương tự (Chẳng hạn lấy thêm các điểm P, Q trên $latex Ox, Oy$ cũng với tính chất AP = BQ để phép quay được xét cũng biến P thành Q) và thay đổi chút ít cách phát biểu cũng như vận dụng tính chất còn lại (tính chất 2) của mệnh đề 2. Ta nhận được:
Bài toán 1. Cho tứ giác ABCD có AB = CD và các điểm M, N trên AB, CD sao cho AM = DN. Giả sử MN cắt AD và BC lần lượt tại P, Q. Chứng minh rằng tồn tại một điểm O có cùng phương tích với tất cả bốn đường tròn ngoại tiếp các tam giác PSAM, PDM, QBM, QCN.

Lời giải. Gọi O là tâm của phép quay R biến AB tương ứng thành CD và M thành N. Theo mệnh đề 3 (tính chất 2) các tứ giác AMOP, ANOP, BMOQ, CNOQ đều nội tiếp. Khi đó O nằm trên 4 đường tròn ngoại tiếp các tam giác PAM, PAN, BMQ và CNQ nên có cùng phương tích đối với các đường tròn này.
2.2. Tích của hai phép quay. Điều cần bổ sung thứ hai liên quan đến bản chất ánh xạ của các phép biến hình. Một khi đã định nghĩa chúng như các ánh xạ thì lẽ tự nhiên cũng cần phải đề cập đến tích của hai phép biến hình. Vậy tích của hai phép quay là gì?
Mệnh đề 2.6. Cho hai phép quay $latex R_1(O_1, \alpha_1), R_2(O_2, \alpha_2)$. Nếu $latex \alpha_1 + \alpha_2 \neq 2k\pi$ thì tích $latex R = R_2.R_1$ là một phép quay với góc quay $latex \alpha = \alpha_1 + \alpha_2$. Tâm $latex O$ của phép quay được xác định dựa vào điều kiện sau:
$latex \widehat{(\overrightarrow{O_1O}; \overrightarrow{O_1O_2})} = \dfrac{\alpha_1}{2}, \widehat{(\overrightarrow{O_2O}; \overrightarrow{O_2O_1})} = \dfrac{\alpha_2}{2}$
 Chứng minh. Việc R là phép quay có thể suy ra ngay từ mệnh đề 1. Còn tâm O chính là điểm bất động duy nhất qua tích $latex R = R_2.R_1$. Nếu chọn điểm O như trên và lấy $latex O’$ đối xứng của $latex O$ qua $latex O_1O_2$ thì ta có $latex R_1(O) = O’, R_2(O’) = O$, suy ra $latex R(O) = O$. Vậy điểm O được xác định như trên chính là tâm quay.
Chứng minh. Việc R là phép quay có thể suy ra ngay từ mệnh đề 1. Còn tâm O chính là điểm bất động duy nhất qua tích $latex R = R_2.R_1$. Nếu chọn điểm O như trên và lấy $latex O’$ đối xứng của $latex O$ qua $latex O_1O_2$ thì ta có $latex R_1(O) = O’, R_2(O’) = O$, suy ra $latex R(O) = O$. Vậy điểm O được xác định như trên chính là tâm quay.
Bài tập sau có thể xem là ứng dụng mẫu mực của việc vận dụng tích 2 phép quay:
Ví dụ 2.7. Bên ngoài tam giác ABC và trên các cạnh dựng các tam giác $latex BCA_1, CAB_1, ABC_1$ cân lần lượt tại $latex A_1, B_1, C_1$ với góc $latex \widehat{BA_1C} = 260^o$ và các góc $latex \widehat{CB_1A} = \widehat{AC_1B} = 100^o$. Tính góc $latex \widehat{B_1A_1C_1}$
 Bài tập này được giải quyết hết sức nhanh gọn và sáng sủa từ mệnh đề trên. Trước hết, nhận xét rằng: $latex R(A_1; – 160^o) = R(B_1; 100^o)o R(C_1; 100^o)$
Bài tập này được giải quyết hết sức nhanh gọn và sáng sủa từ mệnh đề trên. Trước hết, nhận xét rằng: $latex R(A_1; – 160^o) = R(B_1; 100^o)o R(C_1; 100^o)$
Theo tính chất tâm của tích hai phép quay thì: $latex \widehat{(\overrightarrow{C_1A_1}, \overrightarrow{C_1B_1})} = \widehat{(\overrightarrow{B_1C_1},\overrightarrow{B_1A_1})} = \dfrac{100^o}{2} = 50^o$
Vì vậy $latex \widehat{B_1A_1C_1} = 80^o$
Tất nhiên với đề bài như trên, một số học sinh vẫn có thể đi “tính được” góc $latex \widehat{B_1A_1C_1}$ với một khối lượng tính toán hết sức cồng kềnh và với kỹ thuật tính toán đáng nể. Nếu bây giờ biết tấu bài tập này đi một chút bằng cách cất đi điểm mấu chốt $latex A_1$ và gắn têm tính di động cho các điểm $latex B_1C_1$ thì có thể nhận được phương án sau:
Bài toán 2. Cho tam giác ABC nội tiếp đường tròn (O) có B, C cố định, còn A thay đổi trên (O). Bên ngoài tam giác, trên các cạnh AB, AC dựng các tam giác $latex ABC_1, ACB_1$ lần lượt cân tại $latex C_1, B_1$ với $latex \widehat{AC_1B}=\widehat{AB_1C}=100^o$. Chứng minh rằng trung trực của $latex B_1C_1$ luôn đi qua một điểm cố định. $latex \angle$
Rõ ràng điểm cố định cần tìm chính là điểm A 1// trong bài tập trên nay đã được “giấu” đi. Và chính vị trí không dễ đoán của A 1// đã làm cho bài toán trở nên vô cùng khó khăn cho những ai chưa nắm được ý tưởng về tích của hai phép quay.
2.3. Về các phép dời hình khác. Để kết thúc phần này, xin nêu ra điều cần bổ sung cuối cùng để cho nội dung về phép biến hình được cân đối, hoàn chỉnh. Chúng ta biết rằng lớp các phép biến hình được trình bày đầy đủ nhất chính là lớp các phép dời hình. Chúng có thể được mô tả rất trọn vẹn thông qua các phép dời hình cơ sở là tịnh tiến, quay và đối xứng trục. Vậy nên chăng sau khi đã học xong các phép biến hình cụ thể này, chúng ta sẽ khái quát bằng khái niệm các phép dời hình và kết thúc bằng một mệnh đề mô tả đầy đủ lớp các phép dời hình để làm sáng tỏ bản chất khá đơn giản của chúng. Đây thường là sơ đồ mẫu mực khi trình bày về một lớp các phép biến đổi nào đó trong các lĩnh vực khác của toán học.
Mệnh đề mô tả các phép dời hình ở đây rất gọn, đơn giản và có thể suy ra trực tiếp từ Mệnh đề 1 ở trên. Nhưng trước khi phát biểu nó, theo tôi nên phân loại các phép dời hình thành các phép dời hình thuận (là các phép dời hình bảo toàn định hướng) và các phép dời hình ngược (thay đổi định hướng). Điều này cũng gần giống như việc phân biệt hai tam giác bằng nhau thuận và bằng nhau nghịch mà học sinh đã rất quen thuộc. Việc phân loại các phép dời hình như vậy sẽ không gây ra khó khăn nào mà trái lại, nó còn có thể giúp học sinh hiểu và cảm nhận rõ ràng hơn về định hướng (cụ thể là chiều “quay” của một tam giác) trong các phép biến hình.
Đối với các phép dời hình thuận (quan trọng nhất và được xem xét kỹ lưỡng nhất) ta có sự mô tả đầy đủ sau:
Mệnh đề 2.8. Một phép dời hình thuận chỉ có thể là một phép tịnh tiến hoặc một phép quay.
Đối với các phép dời hình nghịch thì khó khăn hơn một chút:
Mệnh đề 2.9. Một phép dời hình nghịch có thể được biểu diễn như là tích một phép tịnh tiến với một phép đối xứng trục.
Trong phần bài tập của bộ sách giáo khoa Hình học nâng cao lớp 11, dạng tích này cũng được xét đến và được gọi là phép “đối xứng trượt”. Theo tôi, Mệnh đề 2.9 có thể không nhất thiết phải trình bày hoặc chỉ cần nhắc qua và đưa ra như một bài tập. Nhưng Mệnh đề 2.8 thì nên phát biểu như một lời đúc kết của phần các phép dời hình để sao cho khi học xong phần này, học sinh có cảm giác nắm bắt trọn vẹn, rõ ràng, không còn chút gì mơ hồ về các phép dời hình.
(Còn nữa) [Phần 2]